¡FOTOS REALIZADAS EN MONUMENTOS CON EL

NÚMERO CORDOBÉS!

LA TORRE MAL MUERTA

OFICINAS DE CAJA SUR EN EL BULEVAR

EL ARQUITECTO RAFAEL DE LA HOZ ARDERIUS


Nace en Madrid en 1924. Su infancia transcurre en Córdoba, donde también comienza su carrera profesional. Fue un gran aficionado a las matemáticas durante toda su vida, y como curiosidad, su Conferencia en la Quinta Asamblea de Instituciones de Cultura de las Diputaciones Provinciales titulada ``La proporción cordobesa´´, referida al numero que nos da la relación de proporcionalidad entre el radio y el lado de un octógono, y que se puede encontrar editada en un libro con el mismo nombre.

En Madrid acabó sus estudios de Arquitectura (1951). Entre los años 1981 y 1985 fue Presidente de la Unión Internacional de Arquitectos. En 1985 continua su formación en el Instituto Tecnológico de Massachussets. En 1990 es nombrado Académico de Bellas Artes. Su primer trabajo como arquitecto fue para construir en Córdoba el local comercial de Vogue.
Junto al también arquitecto José María García Paredes participó en el proyecto de la Cámara de Comercio de Córdoba, y también en el Colegio Mayor Aquinas en Madrid por el que recibieron el Premio Nacional de Arquitectura. Más tarde su estudio de arquitectura se encargaría de proyectos como la fábrica de cervezas El Águila (Córdoba), el Palacio de Congresos de Torremolinos, la sede del Colegio de Médicos de Sevilla y el colegio de las teresianas en Córdoba: el colegio Bética-Mudarra.

Después se trasladaría a Madrid, donde continuaría su obra proyectando la ampliación del Ministerio de Marina (el que es hoy edificio de Catalana Occidente en el paseo de la Castellana), la sede de Inserso, o el centro de telefónica en Madrid.

Muere en Madrid en junio del año 2000. Continuación exhibimos una redacción de algunos de sus proyectos y premios más importantes.





ALGUNOS PROYECTOS:


1951 Tienda Vogue, Córdoba, España
1951 Proyecto centro comercial El Brillante ,Córdoba ,España.
1953-1957 colegio Mayor Aquinas , Madrid, España.
1954 Tintorería Lindsay, Córdoba ,España.
1954 chalet La Cabaña ,Córdoba, España.
1955 viviendas calles Pastores,Córdoba, España.
1955-1958 Edificio de viviendas Calle Cruz Conde, Córdoba.
1956 Oficinas del Banco Popular, Córdoba, España.
1956-1958 Farmacia E.Grande, Córdoba, España.
1957 Tienda de Helados Navarro, Córdoba, España.

PREMIOS:

1956 Premio Nacional de Arquitectura (Colegio Mayor Aquinas).
1995 VI Premio Antonio Camuñas de Arquitectura.
2000 Medalla de Oro de la Arquitectura.


MAS SOBRE MONUMENTOS

Córdoba no es ajena a el uso de la construcción del octógono en la construcción como podemos observar, es mas , parece como si sus arquitectos encontrasen una especial satisfacción en esta figura geométrica.
La solución constructiva de la universalmente llamada ``bóveda cordobesa´´ que se inventa en la mezquita, tiene planta octogonal.

Y efectivamente como hemos observado, y ya comentábamos anteriormente, el uso de la proporción cordobesa es un elemento básico en la arquitectura califal cordobesa y en la posterior, pero también se refleja en construcciones anteriores como en las Pirámides de Egipto o en mundos``no siempre conocidos´´ como en las pirámides de Teotihuacan.
Aparece en templos cristianos(iglesias-catedrales), judíos (sinagogas) y musulmanes(mezquitas).

Tanta coincidencia atemporal, universal e intercultural no puede ser fruto de la aleatoriedad(``No creo que juegue a los dados con el mundo´´,decía A.Einstein), sino un ordena natural , un orden natural humano.

UN POCO DE HISTORIA:

En el siglo noveno despues de Cristo "Los Elementos" de Euclides fue traducido en las escuelas de Córdoba.
Córdoba fue depositaria y única usufructuaria del tesoro euclidiano durante la Edad Media.
Esta situación de privilegiado monopolio terminó por una de las primeras operaciones de espionaje científico que se tiene memoria. En 1120, el británico Adelardo de Bath, previamente adiestrado en el idioma, usos y costumbres y disfrazado de estudiante hispano-árabe, logró introducirse en nuestras escuelas y sacar una copia de "Los Elementos" que fue publicada en 1472.
Hasta 1535, año en que se descubre el texto griego, Europa no cuenta más que con esta traducción árabe.
Con estos antecedentes, era razonable pensar que si en alguna arquitectura pre-renacentista se había empleado racionalmente la proporción áurea, este lugar no podía ser otro que Córdoba.

CURIOSIDADES!

En unas pruebas realizadas en 1951 en la Diputación de Córdoba, se realizó un test a estudiantes de arquitectura en que se pedía que dibujaran el rectángulo ideal, dando a priori una mayor puntuación a quien racional o instintivamente dibujara el áureo, se detectó que la mayoría había trazado uno, menos esbelto que el armónico, con la proporción aproximada de 1,3.

El hecho era suficientemente significativo para ser investigado. La repetición del test con personas nacidas o residentes en Córdoba conducía reiteradamente a esa proporción. La frecuencia de la proporción 1,3 desbordó la debida al cálculo de probabilidades.

Bien podía suceder que si bien el hombre ideal davinciano debería ser de proporciones divinas, el hombre cordobés es según sus propias características étnicas humano.
El estudio antropométrico en el tallado militar y en las figuras de relieves, esculturas o mosáicos romanos condujo a que los cordobeses romanos han gustado de proporcionar sus figuras humanas según la constante 1,3.

CONSTRUCCION DEL RECTANGULO CORDOBES

Teniendo en cuenta el apartado anterior es muy fácil construir un rectángulo en la proporción cordobesa.
Basta con trazar una circunferencia y la bisectriz del primer cuadrante. RT es un lado del rectángulo y el radio de la circunferencia el otro.

DETERMINACION SOBRE LA RECTA REAL DEL NUMERO CORDOBES

Consideramos el segmento unidad y trazamos una circunferencia de radio (2)1/2 La bisectriz del ángulo MOM' corta a dicha circunferencia en C'. Proyectando sobre la recta real obtenemos C.

En efecto:

En el triángulo OCC'

Observa que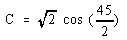
es la expresión trigonométrica del número cordobés.

FUNDAMENTOS GEOMETRICOS SOBRE EL OCTOGONO REGULAR

Consideremos la circunferencia de radio R. Si trazamos la bisectriz del primer cuadrante, el segmento NP = X es el lado del octógono regular inscrito en dicha circunferencia. Aplicando el teorema de Pitágoras al triángulo NOM resulta que
por lo que: (MN)2 = R2 + R2

Por simetría OP' = MN/2 (ya que NP'= MN/2 y OP' = P'N) Como QNP es recto, aplicando el teorema del cateto resulta:
X /QP = P'P/ X

de donde
X2 = QP. P'P = 2R (OP - OP') es decir:

De esta expresión deducimos (considerando la circunferencia de radio unidad, radio R = 1) que:

EL NÚMERO CORDOBÉS!

¿QUE ES EL NÚMERO CORDOBÉS?

En diversos trabajos de investigación (de arquitectura, sobre pintura, etc.) aparece un rectángulo que no está en la proporción áurea, sino que la relación entre sus lados es de 1,3... (Sin ir más lejos, si la resolución de tu ordenador es de 800x600, se encuandra en la misma proporción)

Si el número áureo puede establecerse como la relación existente entre el lado del decágono regular y el radio de la circunferencia circunscrita al mismo, pareció lógico buscar una relación de la misma naturaleza con la que dicha proporción quedara geométricamente fundamentada. La misma quedó establecida al obtener la proporción buscada como la relación entre el radio de la circunferencia circunscrita al octógono regular y el lado de éste.

Cualquier matemático, o buen aficionado, sabe que esta relación es:

Dicho cociente es c = 1,306562964 ... que se conoce como número cordobés Al ser más fácil construir un octógono regular que un pentágono, dicha proporción se extendió rápidamente quedando de manifiesto en múltiples obras pictóricas y arquitectónicas.

PROPORCIÓN AÚREA

Recordando que la proporción áurea es la existente entre el lado y el radio del decágono, que la cuadradad es la misma relación referida al exágono y que la raíz de dos es la resultante del cuadrado, se concluye que la serie de polígonos regulares de 10, 6 y 4 lados, origen de las proporciones conocidas quedaría completa con la inclusión del octógono:

resultando un número irracional prácticamente igual al determinado empíricamente.